布隆过滤器（Bloom Filter）由布隆于 1970 年提出，它实际上由一个很长的二进制向量和一系列随机映射函数组成。布隆过滤器可以用于查询一个元素是否在一个集合中，它的优点是空间和时间效率都远超一般的算法，缺点是会有一定的误判和删除困难。

概要介绍

布隆过滤器

直观的说，bloom 算法类似一个 Hash Set，用来判断某个元素（key）是否在某个集合中。和一般的 Hash Set 不同的是，这个算法无需存储 key 的值，对于每个 key，只需要 k 个比特位，每个存储一个标志，用来判断 key 是否在集合中。

优点：

存储空间和插入/查询时间都是常数。
Hash 函数相互之间没有关系，方便由硬件并行实现。
布隆过滤器不需要存储元素本身，在某些对保密要求非常严格的场合有优势。
布隆过滤器可以表示全集，其它任何数据结构都不能。
k 和 m相同，使用同一组散列函数的两个布隆过滤器的交并差运算可以使用位操作进行。
在增加了错误率这个因素之后，布隆过滤器通过允许少量的错误来节省大量的存储空间。

对于一个有 1% 误报率和一个最优 k 值的布隆过滤器来说，无论元素的类型及大小，每个元素只需要 9.6bits 来存储。如果 1% 的误报率太高，那么对每个元素每增加 4.8bits，可将误报率降低为 0.1%。

缺点：

有误判的可能，即存在 False Position。
无法对已存内容进行获取或者删除。

适用场景

由于布隆过滤器有一定几率的误判，因此不适用于对数据准确要求度极高的场合。

常用的解决方案：

垃圾邮件过滤
爬虫时 URL 重复
缓存穿透上的应用：少量的漏网之鱼要比大量穿透好得多

有效的技术方案：

Google 的分布式数据库 Bigtable 使用了布隆过滤器来查找不存在的行或列，以减少磁盘查找的 IO 次数
Squid 网页代理缓存服务器在 cache digests 中使用了布隆过滤器
Venti 文档存储系统采用布隆过滤器来检测先前存储的数据
SPIN 模型检测器使用布隆过滤器在大规模验证问题时跟踪可达状态空间
Google Chrome 浏览器使用了布隆过滤器加速安全浏览服务
Google Guava - 使用 bloom 过滤器判断是否存在该行（rows）或（colums），以减少对磁盘的访问，提高数据库的访问性能
Apache HBase - 使用 bloom 过滤器判断是否存在该行（rows）或（colums），以减少对磁盘的访问，提高数据库的访问性能
Apache Cassandra - 使用 bloom 过滤器判断是否存在该行（rows）或（colums），以减少对磁盘的访问，提高数据库的访问性能
比特币 - 使用布隆过滤判断钱包是否同步OK

下图是在 Key-Value 系统中布隆过滤器的典型使用：

原理分析

位图

位图，就是用每一位来存放某种状态，适用于大规模数据，但数据状态又不是很多的情况。通常是用来判断某个数据是否存在的。

位图其实是用数组实现的，数组的每一个元素的每一个二进制位都可以表示一个数据的状态，1 表示数据存在，0 表示数据不存在。

位图的数据结构

public class BitMap { // Java中char类型占2个字节，即16bit
  private char[] bytes; // 我们使用char类型作为存储二进制的基本类型
  private int nbits;
  
  public BitMap(int nbits) {
    this.nbits = nbits; // 一共有 nbits 个二进制位需要保存
    this.bytes = new char[nbits/16+1]; //  一个 char 可以保存 16 个 bit ，所以需要 nbit/16+1 个 char
  }

  public void set(int k) {
    if (k > nbits) return;
    int byteIndex = k / 16; // 计算 k 会落到哪个 char 上，即在 char[ k / 16 ] 中包含了 k
    int bitIndex = k % 16; // 计算 k 会落到 char 到哪一位上，即 char[k / 16] 中的第 k % 16 -1 个 bit （-1是因为数组从 0 开始计数）
    bytes[byteIndex] |= (1 << bitIndex);
  }

  public boolean get(int k) {
    if (k > nbits) return false;
    int byteIndex = k / 16; // 同上
    int bitIndex = k % 16; // 同上
    return (bytes[byteIndex] & (1 << bitIndex)) != 0;
  }
}

位图的问题

如果数据的范围较小，位图的性能较好。但如果数据范围在一个很大的区间，数组实现的位图可能会受到操作系统等的各种限制，并且也极耗费内存。针对这个问题，解决方案就是布隆过滤器。

布隆过滤器

布隆过滤器的思想，是在位图中添加多个哈希函数，减小需要开辟的存储空间。

布隆过滤器基本原理

设计一个f(x) = x % n的哈希函数（x 代表数字，n 代表你想要开辟的存储空间），就可以将需要开辟的空间大小缩小为max(x) % n倍。

当然，使用哈希函数一大问题是会存在散列冲突，针对这种情况，我们可以使用多个哈希函数共同确定一个一个数是否存在：

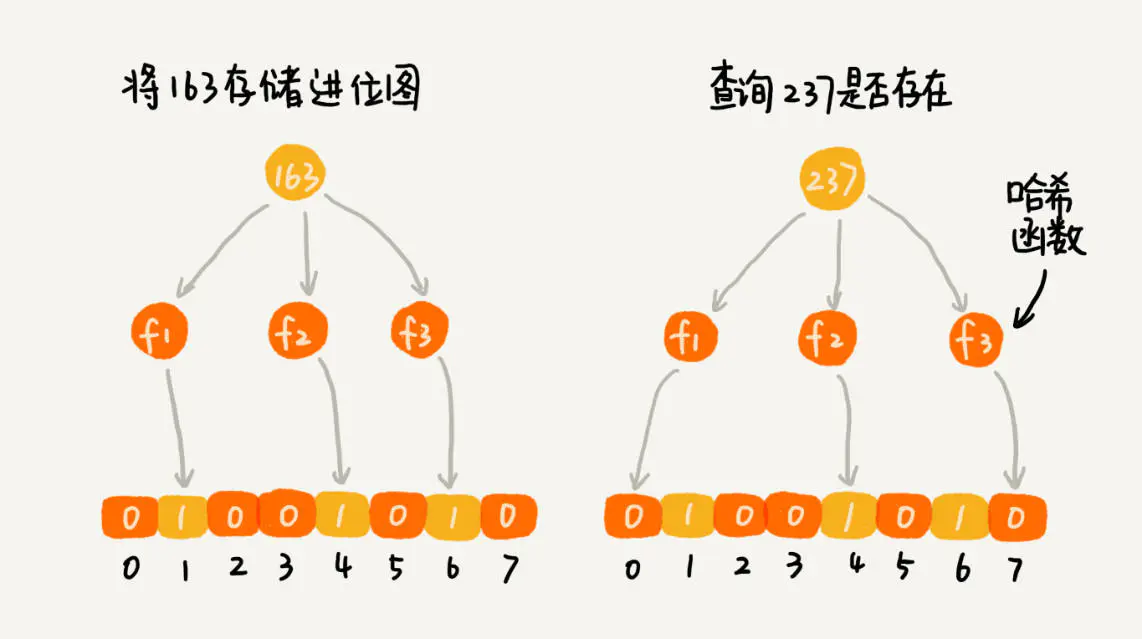
我们使用 K 个哈希函数，对同一个数字进行求哈希值，那会得到 K 个不同的哈希值，我们分别记作 X1，X2，X3，…，XK。我们把这 K 个数字作为位图中的下标，将对应的 BitMap[X1]，BitMap[X2]，BitMap[X3]，…，BitMap[XK] 都设置成 true，也就是说，我们用 K 个二进制位，来表示一个数字的存在。
当我们要查询某个数字是否存在的时候，我们用同样的 K 个哈希函数，对这个数字求哈希值，分别得到 Y1，Y2，Y3，…，YK。我们看这 K 个哈希值，对应位图中的数值是否都为 true，如果都是 true，则说明，这个数字存在，如果有其中任意一个不为 true，那就说明这个数字不存在。

基本原理如下图：

布隆过滤器的缺陷

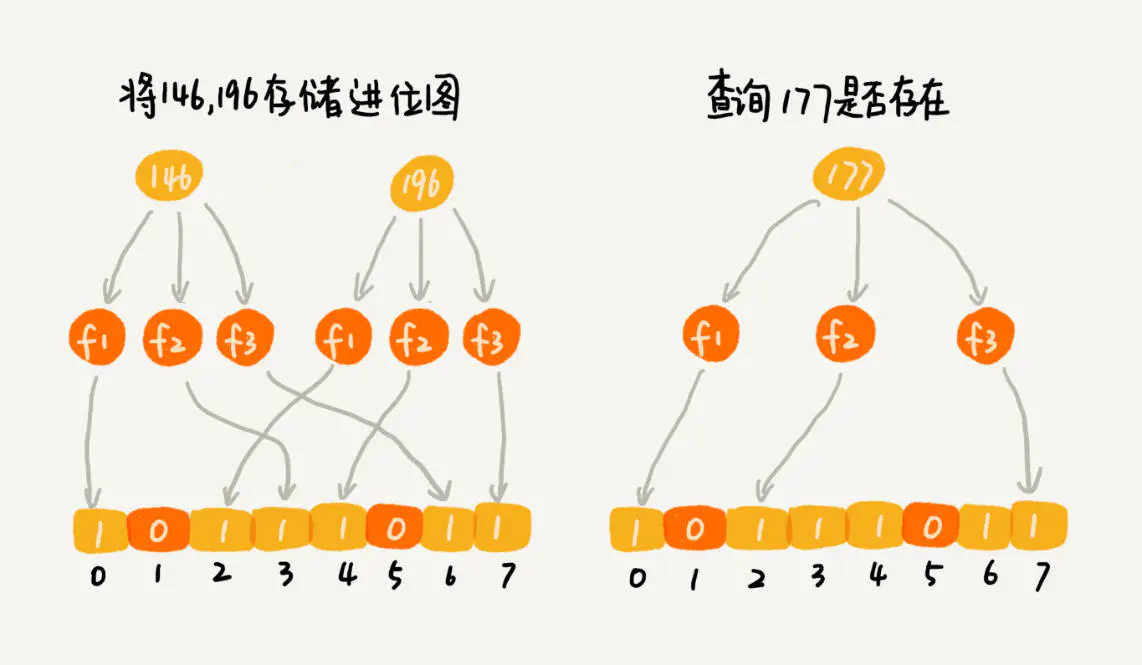
需要注意的是，布隆过滤器可能会出现判断错误的情况

但根据哈希的原理，可知布隆过滤器会将不存在的数据误判为存在。不过，只要调整哈希函数的个数、位图大小跟要存储数字的个数之间的比例，那就可以将这种误判的概率降到非常低。

基本原理如下图：

所以，布隆过滤器只能使用在可以容忍一定错误的情境下。

误算率（False Positive）推导

假设：布隆过滤器中的 Hash 函数满足简单均匀散列，元素都等概率地散列到所有桶中的任何一个

记号：

k — 布隆过滤器中 Hash 函数的个数

m — 布隆过滤器中全部 bit 位的个数

n — 布隆过滤器中存在 bit 位的个数

m、n、k相关性

假设 Hash 函数以等概率条件选择并设置 Bit Array 中的某一位，那么位数组中某一特定的位在进行元素插入时的 Hash 操作中没有被置位的概率是：$1-\frac{1}{m}$，那么在所有 k 次 Hash 操作后该位都没有被置 “1” 的概率是：$(1-\frac{1}{m})^k$。如果我们插入了 n 个元素，那么某一位仍然为 “0” 的概率是：$(1-\frac{1}{m})^{kn}$，因而该位为 “1”的概率是：$1-(1-\frac{1}{m})^{kn}$。

现在检测某一元素是否在该集合中。标明某个元素是否在集合中所需的 k 个位置都按照如上的方法设置为 “1”，但是该方法可能会使算法错误的认为某一原本不在集合中的元素却被检测为在该集合中（False Positives），该概率由以下公式确定：

$(1-(1-\frac{1}{m})^{kn})^k\approx(1-e^{-kn/m})^k \quad根据 \lim_{x \to \infty}{(1-\frac{1}{x})^{-x}=e}$

其实上述结果是在假定由每个 Hash 计算出需要设置的位（bit）的位置是相互独立为前提计算出来的，不难看出，随着 m （位数组大小）的增加，假正例（False Positives）的概率会下降，同时随着插入元素个数 n 的增加，False Positives 的概率又会上升。

对于给定m、n，k为何值可以使误判率最低

设误判率f(k)的函数为：$f(k)=(1-e^{-\frac{nk}{m}})^k$

设$b=e^{n/m}$，则简化为$f(k)=(1-b^{-k})^k$
两边取对数，$lnf(k)=k \times ln(1-b^{-k})$
求导化简后，得

$b^{-k}=\frac{1}{2} \Rightarrow e^{-\frac{kn}{m}}=\frac{1}{2} \Rightarrow k=ln2\frac{m}{n}\approx0.7\frac{m}{n}$

当 k 等于上述推论时，此时误判率最低。若想保持某固定误判率不变，布隆过滤器的比特数 m 与被加的元素数 n 应该是线性同步增加的。

此时 False Positives 的概率为：$2^{-k} \approx 0.6185^{m/n}$

False Positives概率 p，如何选择最优的位数组大小 m

$m=-\frac{nlnp}{(ln2)^2}$

上式表明，位数组的大小最好与插入元素的个数成线性关系，对于给定的 m，n，k，假正例概率最大为：

$(1-e^{-k(n+0.5)/(m-1)})^k$

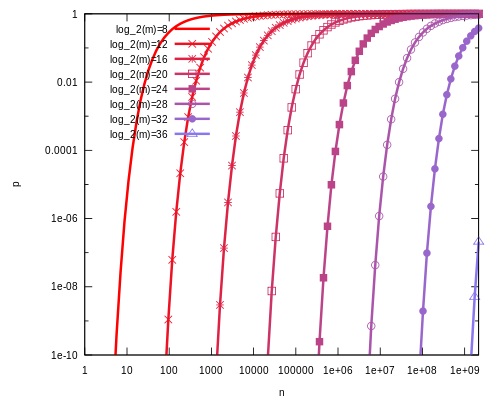
下图是布隆过滤器假正例概率 p 与位数组大小 m 和集合中插入元素个数 n 的关系图，假定 Hash 函数个数选取最优数目：

$k=(m/n) \times ln2$

布隆过滤器性能分析

布隆过滤器在一定条件下可以替代散列表，在空间上，布隆过滤器无疑会减少非常多的空间消耗。而在时间上，它的表现是否依然优秀呢？答案是肯定的：

布隆过滤器用多个哈希函数对同一个资源进行处理，CPU 只需要将网页链接从内存中读取一次，进行多次哈希计算，理论上讲这组操作是 CPU 密集型的。而在散列表的处理方式中，需要读取散列值相同（散列冲突）的多个资源，分别跟待判重的资源，进行匹配。这个操作涉及很多内存数据的读取，所以是内存密集型的。CPU 计算可能是要比内存访问更快速的，所以，理论上讲，布隆过滤器的判重方式，更加快速。

改进方案

Counting Bloom Filter

Counting Bloom Filter 的出现解决了无法删除的问题，它将标准 Bloom Filter 位数组的每一位扩展为一个小的计数器（Counter），在插入元素时给对应的 k（k为哈希函数个数）个 Counter 的值分别加 1，删除元素时给对应的 k个 Counter 的值分别减1， Counting Bloom Filter通过多占用几倍的存储空间的代价，给 Bloom Filter 增加了删除操作。

Spectral Bloom Filter

Spectral Bloom Filter 的出现扩展了出现频率查询的功能。

在 membership query 上，由于 SBF 和 CBF 都沿用 Bloom Filter 的基本结构，因此很难在 membership query 上提高查询效率。但在查询元素出现频率（大于 1 的情况）时，由于 SBF 采用 counter 中的最小值来近似表示元素的出现频率，使得各个 counter 的重要性有所差别，因此 CBF 将 counter 一视同仁的做法就有提高的空间。

优化算法 Minimal Increase

Minimal Increase 算法的思想比较简单。基本思想是：既然在查询元素出现频率时我们只关心 counter 的最小值，那在增加元素时我们就只增加最小值。如果有多个 counter 都是最小值，把它们都增加；如果连续加入 r 个相同的元素，就把最小值（一个或多个 counter ）加 r，其它 counter 的值或者维持不变，或者设为最小值加 r，看哪一个比较大。这种算法是一种聪明的偷工减料：原来增加一个元素时要增加 k（哈希函数个数）个 counter，现在只需要增加最小值。而 counter 的增加次数一旦减少，就意味着 hashing 时碰撞的次数减少，因此查询元素出现频率时出错的可能性也就随之降低。经论文作者证明，Minimal Increase 使查询错误率降低了 k 倍。

当然，偷工减料不可能只有好处。Minimal Increase 最大的弊端就是不支持删除操作。很明显，由于增加元素时增加的 counter 不确定，因此删除元素时也无从下手。如果将 k 个 counter 都减少，就会造成 false negative 的出现（查询结果表明集合不包含某元素而实际上包含）。由于这个严重的弊端，Minimal Increase 的应用前景被大打折扣。

优化算法 Recurring Minimum

Recurring Minimum 算法是既支持增删操作又降低查询错误率的算法。这种算法的基本思想是：发现有可能出错的情况，然后将它们单独处理。

什么是 recurring minimum

SBF 中如果一个元素对应的 k 个 counter 中有一个以上都维持最小值，就称它有 recurring minimum（RM）。我们发现没有 RM（即 single minimum）的元素出现查询错误的概率很高，而有 RM 的元素错误概率很低。因此这种算法将没有 RM 的元素单独处理，在主 SBF 之外又增加了一个辅助的 SBF，专门用来存储这类元素。由于这类元素所占比例不会太大，因此辅 SBF 可以只分配较小的空间，比如主 SBF 的一半大小。

采用 Recurring Minimum 增加元素 x 时，先将 x 在主 SBF 对应的 k 个 counter 的值增加，然后再判断这 k 个 counter 有没有 recurring minimum。如果有，就当什么事都没有发生，直接继续；如果没有，就意味着 x 出错的概率很大，这时我们将 x 存储在辅 SBF 上，counter 的值设为 x 在主 SBF 对应 counter 的最小值。删除元素和上面的操作类似，由于主 SBF 没有受算法的影响，所以不会出现 false negative。在查询一个元素时，先看它在主 SBF 中有没有 recurring minimum。如果有，就返回 counter 的最小值；否则检查辅 SBF 中的 counter 最小值，如果大于 0 就返回这个值，否则返回主 SBF 的值。

由于有 recurring minimum 的情况本来出错概率就很小，而没有 recurring minimum 的情况又单独处理，也大大降低了出错概率，所以整个算法的错误率得以降低。Recurring Minimum 算法的错误率虽然不及 Minimum Increase，但比原来的错误率要好很多，可以说是用更多的空间换取了错误率的大幅降低。

Dynamic Count Filter

Spectral Bloom Filter（SBF）在 Counting Bloom Filter（CBF）的基础上提出了元素出现频率查询的概念，将 CBF 的应用扩展到了 multi-set 的领域。但是，SBF 为解决动态 counter 的存储问题，引入了复杂的索引结构，这让每个 counter 的访问变得复杂而耗时。有没有一种解决方案既支持元素出现频率查询，结构又相对比较简单呢？Dynamic Count Filter（DCF）尝试回答了这个问题。

要支持元素出现频率查询，就需要解决变化范围可能很大的 Counter 的存储问题。DCF 和 SBF 的不同之处，也就是 counter 的存储结构。DCF 使用两个数组来存储所有的 counter，它们的长度都为 m（即 Bloom Filter 的位数组长度）。第一个数组是一个基本的 CBF（即下图中的 CBFV，Counting Bloom Filter Vector），counter 的长度固定，为x = log(M/n)，其中 M 是集合中所有元素的个数，n 为集合中不同元素的个数。第二个数组用来处理 counter 的溢出（即下图中的OFV，Overflow Vector），数组每一项的长度并不固定，根据 counter 的溢出情况动态调整。假设 OFj 是 OFV 中某一项的值，那么 OFV 中每一项的长度y=floor(log(max(OFj))) + 1，即最大值决定了每项长度。

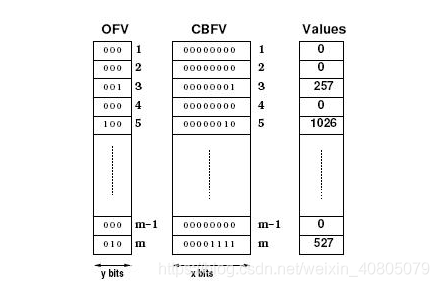
上图中最右一列是 counter 的值，从图中我们可以清楚地看出 OFV 和 CBFV 的作用。比如第 5 个 counter 的值是 1026，二进制为 10000000010。我们把这个二进制位串分成两段 100 和 00000010，分别就对应着 OFV 和 CBFV 中的值。图中我们也可以看出 x + y 就等于 counter 的最大值的二进制位数。

在查询一个 counter 时，DCF 要求两次内存访问。假设想查询位置为 j 的 counter 的值，我们先读出 CBFV 和 OFV 的值，分别为 Cj 和 OFj，那么 counter 的值就可以表示为

$Vj = 2^x \times OFj + Cj$

在集合增加元素时，如果 OFV 的最大值从 2x – 1 增加到2x，OFV就需要给每一项增加1位，否则就会溢出。每次 OFV 大小改变的时候都需要重建。重建是一件开销很大的工作，必须重新创建一个 OFV 数组，然后把旧 OFV 数组的值拷贝到新建的 OFV 数组中，最后把旧 OFV 数组的空间释放掉。如果说增加时的 overflow 必须重建的话，那么集合元素减少时的 underflow 则有更多选择。当 OFV 的最大值从 2x 减少到 2x – 1 时，我们可以选择马上重建 OFV，也可以采用一些策略延迟 OFV 的重建，以避免一些临时性的减少导致 OFV 反复重建。

从上面的介绍可以看出，DCF 中最大的那个 counter 决定了整个结构所占的空间。因此，在 counter 的值普遍不大的情况下，DCF 由于不用维护复杂的索引结构，所以占用空间比 SBF 要少。如果将 counter 的值逐渐增大，SBF 在空间占用上的优势就会越来越明显。在 counter 存取时间上，DCF 占有绝对的优势，只比 CBF 多访问了一次内存。在不同的实际应用场合中对比 SBF 和 DCF，论文作者发现 DCF 整体占用的空间以及执行时间都比 SBF 少了一半还多。

三种方案对比

	Counters Size	Access Time	Rebuilds	Saturated Counters
CBF	Static	fast	n/a	Yes
SBF	Dynamic	slow	high	Eventually
DCF	Dynamic	fast	low	No

Lanchester Blog

Math 布隆过滤器

概要介绍

布隆过滤器

适用场景

原理分析

位图

位图的数据结构

位图的问题

布隆过滤器

布隆过滤器基本原理

布隆过滤器的缺陷

误算率（False Positive）推导

布隆过滤器性能分析

改进方案

Counting Bloom Filter

Spectral Bloom Filter

优化算法 Minimal Increase

优化算法 Recurring Minimum

Dynamic Count Filter

三种方案对比