质数是指在大于 1 的自然数中，除了 1 和它本身以外不再有其他因数的自然数；否则称为合数（规定 1 既不是质数也不是合数），下面一起来欣赏一下质数与其相关定理的魅力吧。

性质

质数的个数是无限的。

(算术基本定理) 任一合数可以分解为有限个质数的乘积，且这种分解是唯一的。

存在性：

待证命题：大于 1 的自然数必可写成质数的乘积。

用反证法：假设存在大于 1 的自然数不能写成质数的乘积，把最小的那个称为 n。

非零自然数可以根据其可除性（是否能表示成两个不是自身的自然数的乘积）分成3类：质数、合数和 1。首先，按照定义，n 大于1。其次，n 不是质数，因为质数 p 可以写成质数乘积：$p=p$，这与假设不相符合。因此 n 只能是合数，但每个合数都可以分解成两个小于自身而大于 1 的自然数的积。设其中 a 和 b 都是介于 1 和 n 之间的自然数，因此，按照 n 的定义，a 和 b 都可以写成质数的乘积。从而 n 也可以写成质数的乘积。由此产生矛盾。因此大于 1 的自然数必可写成质数的乘积。
唯一性

若 n 为正整数，在 $n^2$ 到 $(n+1)^2$ 之间至少有一个质数。

若 n 为大于或等于 2 的正整数，在 $n$ 到 $n!$ 之间至少有一个质数。

若 n 为大于 1 的数，在区间 $(n, 2n]$ 中必存在至少一个质数。

扩展

质性判断

质性判断即精确判断出数的质性。

基本定理判断

质数大于等于 2 不能被它本身和 1 以外的数整除。因此，对于一个大于 1 的整数 n，其质性判断区间为 $(1, n)$。

基本定理优化判断

对于合数 n，我们可以证明它一定有一个小于等于 $\sqrt{n}$ 的非平凡因数。这里的非平凡因数，指的是和1与他本身不同的因数。

假设 n 的所有非平凡因数都是大于 $\sqrt{n}$ 的。任取其中一个和 n 不同的非平凡因数 m，那么存在整数 k 使 $n=km$，那么 k 也为 n 的非平凡因数，但是 $km > \sqrt{n} \times \sqrt{n} = n$，矛盾。所以合数 n 一定有一个小于等于 $\sqrt{n}$ 的非平凡因数。

因此，基于以上证明可将判断区间缩小为 $(1, \sqrt{n})$

eratosthenes筛选法判断

建立一个 bool 型数组 M，若已知一个数 M[k] 是质数，那么其 i（i 为正整数）倍 $M[k * i]$ 必然为合数，可将其去除。

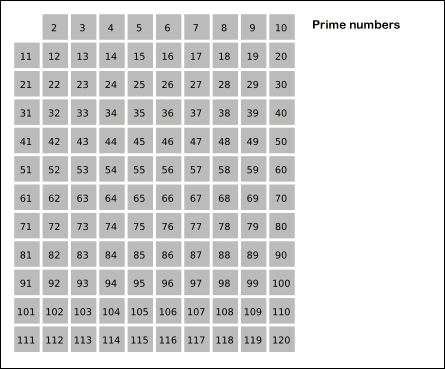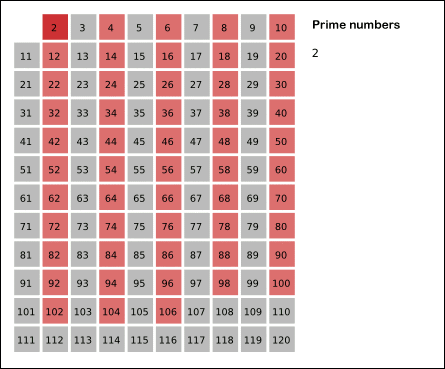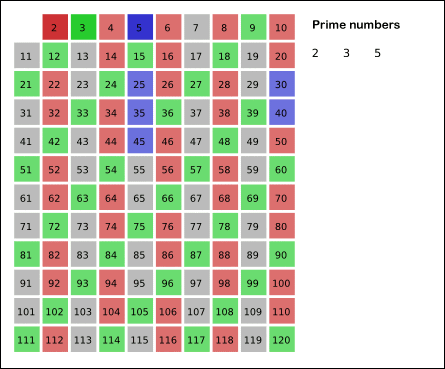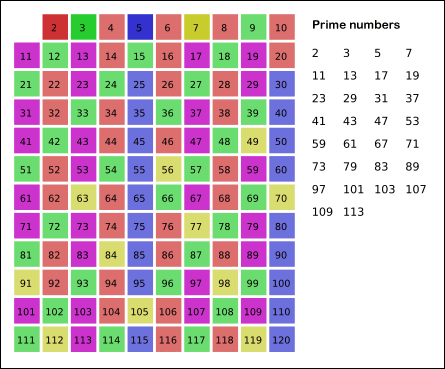
威尔逊定理

在数论中，威尔逊定理给出了判定一个自然是否为素数的充分必要条件，即：当且仅当 p 为素数时：$(p - 1)! \equiv -1 \ (mod \ p)$。$(mod \ p)$ 叫同余意思就是等式两边除以 p 后余数相等，可以把上述式子理解为当且仅当 p 为素数时，[(p - 1)! + 1] % p == 0。

bool isPrime(int n) {
    if (n <= 1) return false;
    int factor = 1;
    for(int i = 2; i < n; ++i)
        factor = ((long long)factor * i) % n;
    factor = (factor + 1) % n;
    return factor == 0;
}

显然这个算法时间复杂度和需要数据类型的表示范围之大都是无法回避的，实际操作不可行，理论价值非常高。

质性检测

质性检测即容忍一定的失误进行质性判断。

素性检测一般用于数学或者加密学领域。用一定的算法来确定输入数是否是素数。不同于整数分解，素性测试一般不能得到输入数的素数因子，只说明输入数是否是素数。大整数的分解是一个计算难题，而素性测试是相对更为容易（其运行时间是输入数字大小的多项式关系）。有的素性测试证明输入数字是素数，而其他测试，比如米勒 - 拉宾（Miller–Rabin ）则是证明一个数字是合数。因此，后者可以称为合性测试。

素性测试通常是概率测试（不能给出100%正确结果）。这些测试使用除输入数之外，从一些样本空间随机出去的数；通常，随机素性测试绝不会把素数误判为合数，但它有可能为把一个合数误判为素数。误差的概率可通过多次重复试验几个独立值 a 而减小；对于两种常用的测试中，对任何合数 n，至少一半的 a 检测 n。的合性，可以通过增加 k 来使得误差尽量小。

常见的检测算法：费马素性检验（Fermat primality test），米勒拉宾测试（Miller–Rabin primality test），Solovay–Strassen测试，卢卡斯-莱默检验法（Lucas–Lehmer primality test）。

费马查表法

在数论中的一个非常重要的定理——费马小定理：假如 a 是一个整数，p 是一个素数，那么 $a^p ≡ a \ (mod \ p) \quad (0<a<p)$。

换句话说也就是：如果 p 是一个素数，且 $0 < a < p$，则 $a ^ { (p - 1) } = 1 \ (mod \ p)$。但是费马小定理是判断素数的必要条件，当 $a = 2$ 时候，有一类伪素数数，它们满足费马小定理，但其本身却不是素数。它们有无穷个，最小的伪素数是 341，统计表明前 10 亿个数中有 50847534 个素数，满足 [2 ^ {(p - 1)}] % p = 1 的伪素数一共有 5597，出错概率非常之低，所以我们可以根据我们的需求建一表伪素数表，算出素数看是否存在这张表里（可以二分，hash，trie）。

如果直接算 $2 ^ {(p - 1)}$ 数的表示范围会溢出，于是我们可以利用这个迭代公式来计算。

int runFermatPower(int a, int b, int n) {//返回a^b mod n
   int result = 1;
 
     for (int i = 0; i < b; i++) {
         result *= a;
         result %= n;
 
   }
   return result;
}

当 b 很大的时候，上述算法效率很一般，下面就引出密码学中一个重要的算法——大数模幂快速算法。

大数模幂快速算法证明：

首先我们要了解以下公式，

a ^ b % m = (...((a % m) * a) % m) ......* a) % m ，其中 a % m 有 b 个

假设，b = 13，

a ^ 13 % m = ((a ^ 8) % m) * ((a ^ 4) % m) * ((a ^ 1) % m)

因此，我们只需要不断右移进行操作就可以。

int runFermatPower(int a, int b, int n)// d≡a^b mod n
{
	int result = 1;
	while (b > 0) {
		if ((b & 1) == 1)
			result = (result * a) % n;
		b >>= 1;
    a = (a * a) % n;
  }
  return result;
}

随后可以进行素数判断

public void femat(int n){
  for(int i = 2; i <= n; i++){
    if(runFermatPower(2, n-1, n) != 1){
      if(i不在伪素数表中)
        输出i;
    }
  }
}

Miller-Rabin素性测试

Miller-Rabin 素性测试是个概率算法，是实践中较常用的算法，它主要基于二次检测定理。Miller-Rabin 算法是一个随机算法，随机生成几个 a 利用费马小定理和二次探测定理来检测素数。

二次探测定理：如果 p 是一个素数,且 $0 < x < p$，则方程 $x * x \equiv 1 \ (mod \ p)$ 的解为 $x = 1, p - 1$。

我们可以把这个二次探测定理加到大数模幂快速算法中

int runFermatPower(int a, int b, int n)// a^b mod n
{
    int result = 1;
		while (b > 0) {
			if ((b & 1) == 1)
				result = (result * a) % n;
			if ((a * a) % n == 1 && a != 1 && a != n - 1)
				return -1;// 二次探测
			b >>= 1;
			a = (a * a) % n;
		}
		return result;
}

Miller-Rabin 检测也存在伪素数的问题，但是与费马检测不同，MR 检测的正确概率不依赖被检测数 p，而仅依赖于检测次数。已经证明，如果一个数 p 为合数，那么 Miller-Rabin 检测的证据数量不少于比其小的正整数的 3/4，换言之，k 次检测后得到错误结果的概率为 $(1/4)^k$

互质关系

如果两个正整数，除了 1 以外，没有其他公因子，我们就称这两个数是互质关系（coprime）。比如，15 和 32 没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。

关于互质关系，不难得到以下结论：

任意两个质数构成互质关系，比如 13 和 61。
一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如 3 和 10。
如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如 97 和 57。
1 和任意一个自然数是都是互质关系，比如 1 和 99。
p 是大于 1 的整数，则 p 和 p-1 构成互质关系，比如 57 和 56。
p 是大于 1 的奇数，则 p 和 p-2 构成互质关系，比如 17 和 15。

欧拉函数及定理

在数论，对正整数 x，欧拉函数是小于 x 的正整数中与 x 互质的数的数目（并定义 $\varphi(1)=1$）。

$\varphi(x) = x \prod _{i = 1} ^n (1 - \frac{1}{p_i})$

(其中 p1, p2……pn 为 x 的所有质因数，x 是不为 0 的整数)

解释：

比如12 = 2 *2 * 3那么 φ(12) = φ(2^2 * 3^1) = 12 * (1 - 1/2) * (1 - 1/3) = 4

即，有 1/2 的数是 2 的倍数，1/3 的数是 3 的倍数，这些数均不与 12 互质。

推论一

如果 $n=1$，则 $\varphi(1) = 1$ 。因为 1 与任何数（包括自身）都构成互质关系。

$\varphi(1) = 1 \times \prod _{i = 1} ^0 (1 - \frac{1}{p_i}) = 1$

推论二

如果 n 是质数，则 $\varphi(n)=n-1$ 。因为质数与小于它的每一个数，都构成互质关系。比如 5 与 1、2、3、4 都构成互质关系。

推论三

如果 n 可以分解成两个互质的整数之积，$n = p1 × p2$ 则 $\varphi(n) = \varphi(p1 \times p2) = \varphi(p1) \times \varphi(p2)$

即积的欧拉函数等于各个因子的欧拉函数之积。比如，$\varphi(56)=\varphi(8×7)=\varphi(8)×\varphi(7)=4×6=24$。

欧拉定理

若n, a为正整数，且n, a互质，则：$a^{\varphi(n)} \equiv 1 \ (mod \ n)$。

记小于 n 且与 n 互质的正整数集合为 $R = \lbrace x1, x_2, …, x{\varphi(n)} \rbrace$。

令 $S = { ax1 \% n, ax_2 \% n, …, ax{\varphi(n)} \% n } = {m1, m_2, …,m{\varphi(n} }$，其中 a 与 n 互质。我们可知这些数有以下性质：

任意两个数 $ax_i \ mod \ n$ 一定不同。

(反证）若存在 $ax_1 \equiv ax_2 \ (mod \ n)$，则 $n | (ax1 - ax2)$。而 a, n 互质且 $x_1 - x_2 < n$，因此 $ax_1 - ax_2$ 不可能被 n 整除，也就是不存在 $ax_1 \equiv ax_2 \ (mod \ n)$。

(数学归纳法) 对于任意的与 n 互质的 $x_i$ 均成立。得证。

那么因为有 $\varphi(n)$ 个这样的数，所以 $x_i \ mod \ n（i=1 ..\varphi(n)）$ 就有 $\varphi(n)$ 个不同的余数。
对于任意的 $ax_i \ mod \ n$ 都与 n 互质。

(反证) $ax_i$ 与 n 互质，假设其余数与 n 有公因子 r，即 $n = r \times (ax_i \ mod \ n)$。则有
$\begin{aligned} ax_i &= p \times n + q \times r \\ &= p \times [r \times (ax_i \ mod \ n)] + q \times r \\ &= r \times [p \times (ax_i \ mod \ n) + q] \end{aligned}$
得出结论 $ax_i$ 与 n 有共同的公因子 r，与条件矛盾。得证。

由上两点证明，集合 S 即无重复值，也全部与 n 互质。因此可推得以下结论：
$S \equiv R \ (mod \ n)$

举例说明一下：

假设集合 R 为与 5 互质的正整数集合 {1, 2, 3, 4}，此时 a 假设为 2。

集合 S = {2 % 5, 4 % 5, 6 % 5, 8 % 5} = {2, 4, 1, 3} = R

在个数不变的情况下，集合内 $ax_i \ mod \ n$ 不重复（证明1）且均与 n 互质，有理由相信，在将 S 进行排序后，与 R 是一一对应的。

此时，我们得出以下等式：

$(a \times x_1) \times (a \times x_2) \times...(a \times x_{\varphi(n)}) \equiv x_1 \times x_2 \times ... x_{\varphi(n)} \ (mod \ n) \\ a^{\varphi(n)} \times (x_1 \times x_2 \times ... x_{\varphi(n)}) \equiv x_1 \times x_2 \times ... x_{\varphi(n)} \ (mod \ n) \\ a^{\varphi(n)} \equiv 1 \ (mod \ n)$

得证，欧拉定理。

费马小定理

费马小定理可以看作欧拉定理的一个特殊情况。假设正整数 a 与质数 p 互质，因为质数 p 欧拉公式为 $\varphi(p)=p-1$ （质数与小于它的正整数均构成互质关系），则可化简为

$a^{p-1} \equiv 1 \ (mod \ p)$

Lanchester Blog

Math 质数之美

性质

扩展